Interaction Nets
An explanation of interaction nets and some examples
What are Interaction Nets?
Interaction nets were introduced in 1990 by mathematician Yves Lafont as a graphical way of representing computations and transformations, generalized from Proof Nets. Interaction nets are graphs of interconnected "agents" that "interact" according to certain rules. These interactions can be evaluated in any order to produce the same final result. They also do not affect other parts of the graph beyond the interacting agents, meaning interactions can be applied in parallel.
Interaction Net Structure
In most interaction nets, agents may have zero or more auxiliary ports, but must have exactly one principal port, which determines interactions (some proposed variations of interaction nets allow more than one principal port). When two agents are connected via their principal ports, they form an active pair, and can be rewritten according to the rules of the interaction system.
Examples
The following examples will use these agent types:
- R: Root agent that connects to the output of the computation
- x and y: Input variables
- AND, OR, and NOT: Boolean logical operators AND, OR, and NOT
- T and F: True and false Boolean values
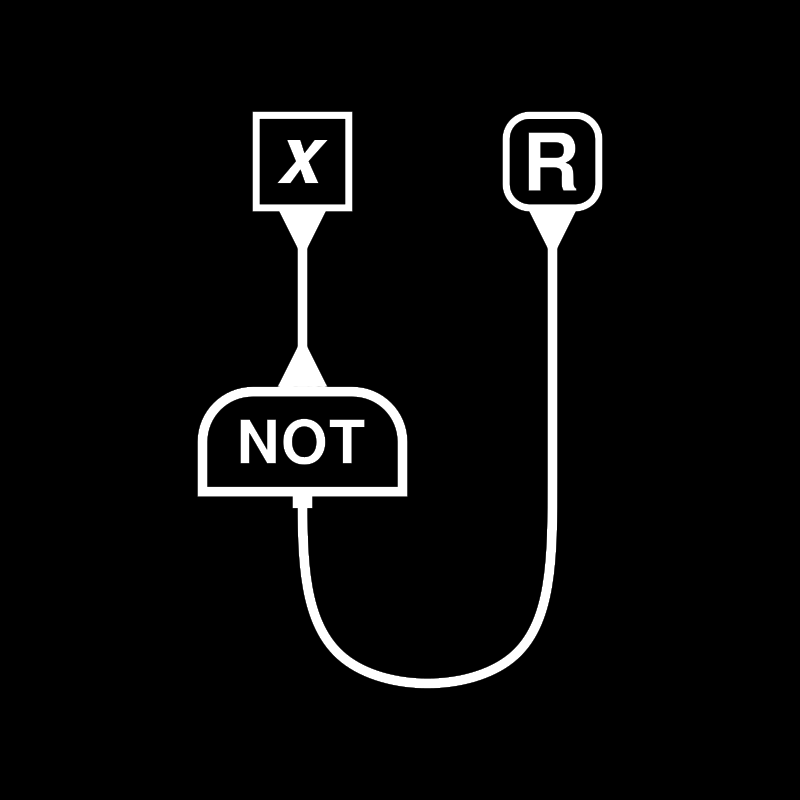
The first example represents a simple interaction net based program to flip Boolean values using the unary agent NOT, which interacts with whatever data is substituted for x, and returns the result through the auxiliary port.
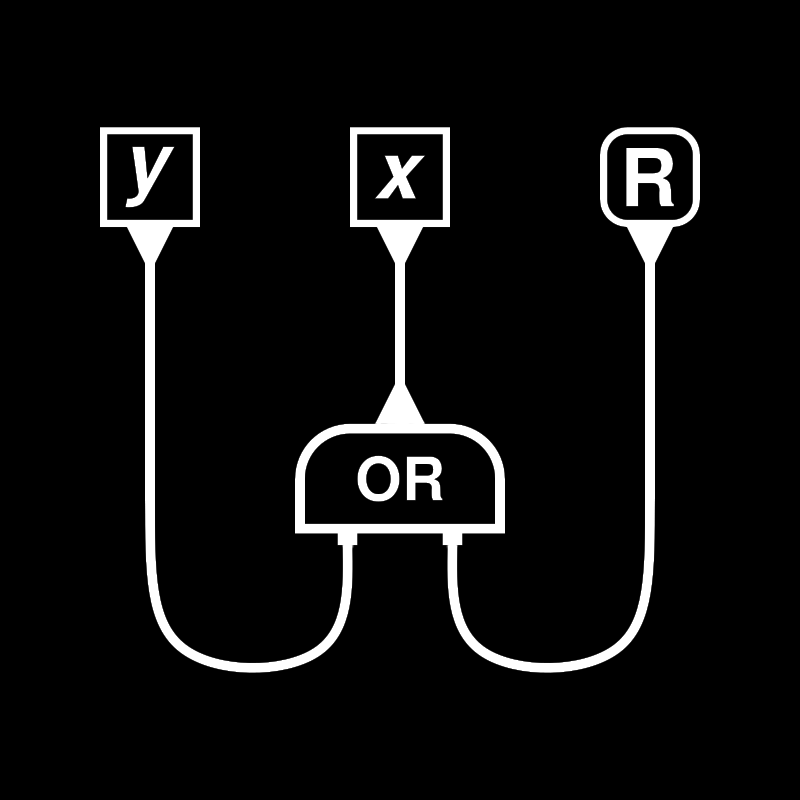
The next example shows a use of the Boolean OR, which rewrites the graph differently based on what boolean it interacts with.
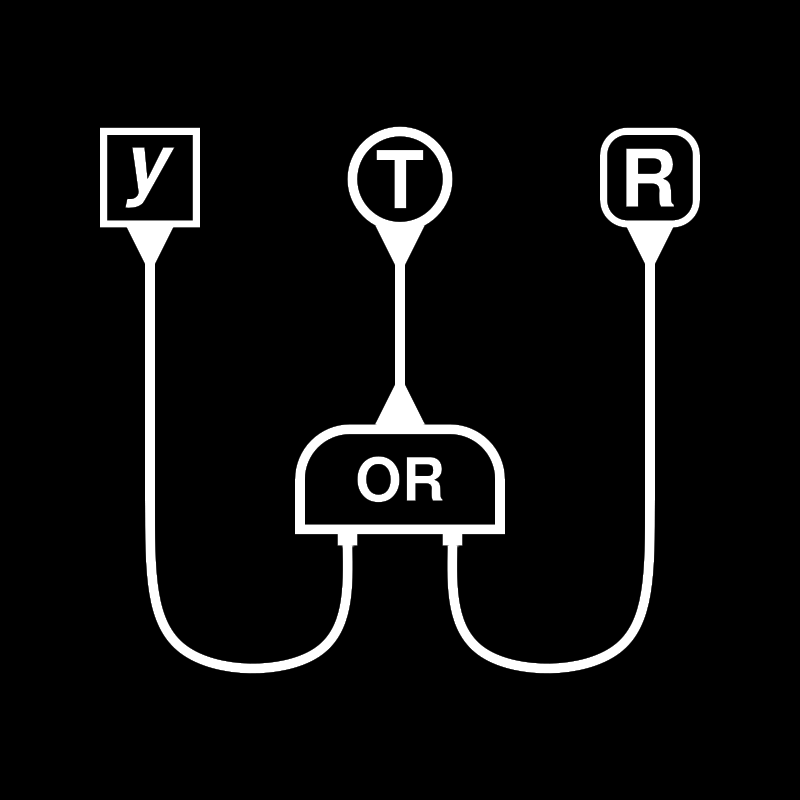
A T (true Boolean value) agent interacting with OR's principal port will directly connect to R.

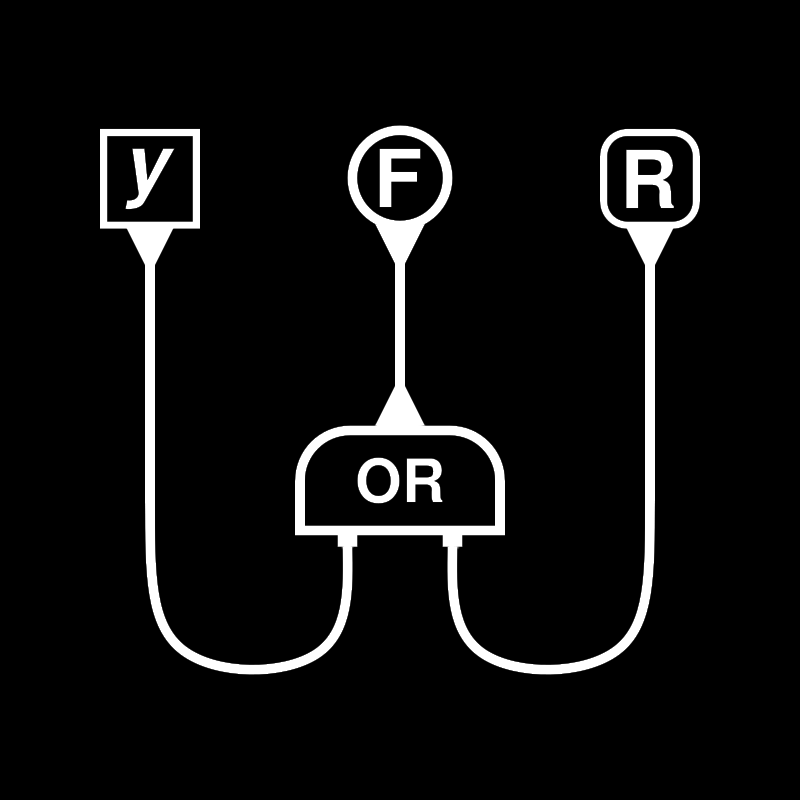
However, as shown below, if the agent connected via OR is F, the graph will be rewritten differently to eliminate the F and the OR, and connect the variable y to R.

Interaction Nets for Optimal Evaluation
The properties of interaction nets make them a very attractive option for designing a runtime or evaluator for automatically parallel computations. A program written for such a runtime could be processed concurrently on the processor's many cores without any additional effort needed for handling synchronization and multithreading issues. This would allow massively parallel execution of code on GPUs too without writing a single line of CUDA or HIP. Machine learning models could be represented as interaction nets to ensure correct and efficient training and inference in a sharded processing environment, such as a datacenter with many interconnected high-performance-compute devices.